Is it possible to predict stock returns using 1 and 12 month historical data? [2021]
![Is it possible to predict stock returns using 1 and 12 month historical data? [2021]](https://firemymoneymanager.com/wp-content/uploads/2021/05/r4.png)
In the 1980s, an economist named Narasimhan Jagadeesh found that historical data — especially 1 and 12 month lagged historical data — can be used via regression to (at least partially) predict stock returns. We run similar tests to determine if this relationship is still true in 2021.
Related articles
Before reading this article, we suggest that you look at Jagadeesh’s paper, as well as a few related articles:
- Evidence of Predictable Behavior of Security Returns
- Common risk factors in the returns on stocks and bonds
- A five factor asset pricing model
- The Cross Section of Expected Stock Returns
Building portfolios to predict stock returns
In his paper, Jagadeesh creates three portfolios to test their returns. These portfolios are S1, S12, and S0.
- S1 is a portfolio based on sorting stocks on their one month lagged return
- S12 is a portfolio based on sorting stocks on their 12 month lagged return
- S0 is a portfolio that uses a regression on the past 12 months, plus a 24 month and a 36 month term to come up with a predicted return. That is then used to sort stocks into portfolios.
For S0, the regression equation is this:

We will perform this regression on each stock over the past decade to find terms a0 to a14. From there, we can (if Jagadeesh’s pattern still holds) partially predict the current month’s return.
Although Jagadeesh didn’t do this, we will group stocks by market cap, allowing us to see if the relationships hold for different size groups.
Writing the code to predict stock returns
We use the following Python code to load the data (this code is based on the code we developed in Getting Started):
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import quandl
import pickle
import csv
from datetime import date
import sys
import statsmodels.api as sm
import scipy.optimize as sco
import scipy.stats as stats
plt.style.use('fivethirtyeight')
np.random.seed(777)
pd.set_option('display.max_rows', 100)
pd.set_option('display.max_columns', 100)
alldata = pd.DataFrame()
pd.set_option('display.max_rows', 100)
pd.set_option('display.max_columns', 100)
try:
ticker_data = pd.read_csv("tickers.csv")
except FileNotFoundError as e:
pass
ticker_data = ticker_data.loc[((ticker_data['table'] == 'SF1') | (ticker_data['table'] == 'SFPY')) & (ticker_data['isdelisted'] == 'N') & (ticker_data['currency'] == 'USD') & ((ticker_data.exchange == 'NYSE') | (ticker_data.exchange == 'NYSEMKT') | (ticker_data.exchange == 'NYSEARCA') | (ticker_data.exchange == 'NASDAQ'))]
for t in ticker_data['ticker']:
if t == 'TRUE': continue
print(t)
try:
data = pd.read_csv(t + ".csv",
header = None,
usecols = [0, 1, 12],
names = ['ticker', 'date', 'adj_close'])
if (len(data) < 2000): #ignore bad data (we have to look into wjhy)
continue
alldata = alldata.append(data)
except FileNotFoundError as e:
pass
tickers = ticker_data['ticker']
df = alldata.set_index('date')
table = df.pivot(columns='ticker')
table.columns = [col[1] for col in table.columns]
t0 = table['2019-01-01':]
t0.index = pd.to_datetime(t0.index)
t0 = t0.resample('BM').last()
dates = t0.index
results = pd.DataFrame(columns = ['r1','r2','r3','r4'])
Next, we will write the code to get the data to perform the regressions. Jagadeesh looks at the following parameters: the past 12 months’ returns, as well as a 24 month and 36 month lagged return.
Note that we choose mega-cap stocks only for our first test. We will explain why later.
We assemble a data frame with each of those parameters, plus the current month’s returns. In the following code, t = -1 gives the current month’s stock price, t = -2 gives the previous month’s stock price, and so on.
Therefore, the current month’s percentage return is (r[t-1] – r[t-2])/r[t-2]. In the following code we look at the percentage return between month t-2 and 12 prior months, scaled to monthly, as well as the return between t-2 and t-26 (the 24 month lag), and t-2 and t-38 (the 36 month lag).
for col in table.columns:
t = table[col]
for m in range(40, len(t)):
idx = t.index[m]
r = t[:idx]
y_i = (r.iloc[-1] - r.iloc[-2]) / r.iloc[-2]
#x_i = [dt1,...dt12]
x_i = []
for j in range(1, 13):
x_i.append( ((r.iloc[-2] - r.iloc[-2-j])/r.iloc[-2-j])/(j) )
x_i.append( ((r.iloc[-2] - r.iloc[-2-24])/r.iloc[-2-24])/24 )
x_i.append( ((r.iloc[-2] - r.iloc[-2-36])/r.iloc[-2-24])/36 )
X.append(x_i)
y.append(y_i)
model = sm.OLS(y, X).fit()
print(model.summary())
The one result for our model from 2009 to 2019 for large companies is:
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.036
Model: OLS Adj. R-squared (uncentered): 0.033
Method: Least Squares F-statistic: 9.490
Date: Mon, 24 May 2021 Prob (F-statistic): 5.10e-21
Time: 17:34:08 Log-Likelihood: 4536.4
No. Observations: 3526 AIC: -9045.
Df Residuals: 3512 BIC: -8959.
Df Model: 14
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 -0.0404 0.023 -1.734 0.083 -0.086 0.005
x2 -0.0633 0.046 -1.365 0.172 -0.154 0.028
x3 0.0730 0.067 1.086 0.278 -0.059 0.205
x4 0.0019 0.086 0.022 0.982 -0.167 0.171
x5 -0.2642 0.105 -2.517 0.012 -0.470 -0.058
x6 0.1934 0.120 1.612 0.107 -0.042 0.429
x7 -0.1831 0.133 -1.381 0.167 -0.443 0.077
x8 0.3311 0.147 2.258 0.024 0.044 0.619
x9 -0.2557 0.159 -1.611 0.107 -0.567 0.056
x10 0.3205 0.170 1.886 0.059 -0.013 0.654
x11 0.1563 0.182 0.861 0.389 -0.200 0.512
x12 -0.0573 0.143 -0.402 0.688 -0.337 0.222
x13 -0.2119 0.112 -1.890 0.059 -0.432 0.008
x14 0.4966 0.153 3.237 0.001 0.196 0.797
==============================================================================
Omnibus: 931.691 Durbin-Watson: 2.028
Prob(Omnibus): 0.000 Jarque-Bera (JB): 13036.841
Skew: 0.863 Prob(JB): 0.00
Kurtosis: 12.260 Cond. No. 23.7
==============================================================================As we can see, the r2 value is pretty low. The F-statistic doesn’t tell us much because our sample size is so large. However, the t-scores of individual months do appear to show some predictive value.
Jagadeesh doesn’t claim that this model predicts individual stock returns, but he does argue that it can be used to predict which stocks will have the highest return. He then creates a portfolio from those stocks and finds that that portfolio outperforms the other portfolios he creates.
To do this, we run the model on each stock in our dataset:
predictions = pd.DataFrame(columns = ['ticker', 'prediction', 'actual'])
for col in table.columns:
r = table[col]
x_i = []
for j in range(1, 13):
x_i.append( ((r.iloc[-2] - r.iloc[-2-j])/r.iloc[-2-j])/(j) )
x_i.append( ((r.iloc[-2] - r.iloc[-2-24])/r.iloc[-2-24])/24 )
x_i.append( ((r.iloc[-2] - r.iloc[-2-36])/r.iloc[-2-24])/36 )
y_i = (r.iloc[-1] - r.iloc[-2]) / r.iloc[-2]
m = model.predict(x_i)
predictions.loc[len(predictions)] = [
col,
m[0],
y_i
]
r = np.array_split(predictions.sort_values("prediction"), 5)
print(str(r[0].mean()))
print(str(r[1].mean()))
print(str(r[2].mean()))
print(str(r[3].mean()))
print(str(r[4].mean()))
results.loc[len(results)]= [
r[0].mean()['actual'],r[1].mean()['actual'], r[2].mean()['actual'], r[3].mean()['actual'], r[4].mean()['actual']
]
preds.loc[len(preds)]= [
r[0].mean()['prediction'], r[1].mean()['prediction'], r[2].mean()['prediction'], r[3].mean()['prediction'], r[4].mean()['prediction']
]
Now, we can look at average monthly returns for the different strata:
In [33]: results.mean()
Out[33]:
r1 0.010521
r2 0.011707
r3 0.016929
r4 0.021485
dtype: float64So r4 does have the highest returns, as predicted by Jagadeesh. However, the model’s actual price predictions are generally inaccurate:
preds.mean()
Out[38]:
r1 0.001676
r2 0.005987
r3 0.010566
r4 0.021798
dtype: float64So can we predict stock returns?
It certainly looks like with just momentum we can’t predict stock returns. But it appears that we can get a reasonable sense of which stocks will do better in the near term.
Let’s look at some details about our predictions. Here are histograms of each quantile:

r1 results 
r2 results 
r3 results 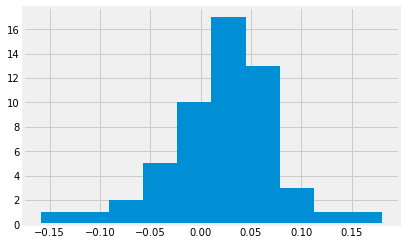
r4 results
To determine whether these are indeed different distributions (not just sampling variations), we can use a KS test. The test should give a p-value of less than our cutoff (let’s say 95%) if these are definitely different distributions. Let’s look at the pairwise results:
stats.ks_2samp(results['r4'], results['r1'])
Out[53]: KstestResult(statistic=0.18518518518518517, pvalue=0.3148816042088447)
stats.ks_2samp(results['r4'], results['r3'])
Out[54]: KstestResult(statistic=0.18518518518518517, pvalue=0.3148816042088447)
stats.ks_2samp(results['r4'], results['r2'])
Out[56]: KstestResult(statistic=0.16666666666666666, pvalue=0.4447065193273601)So the results aren’t significant enough to be confident that these are not just sampling variations.

No Comments