Does pairs trading still work (if you’re not a hedge fund)? [2021]
![Does pairs trading still work (if you’re not a hedge fund)? [2021]](https://firemymoneymanager.com/wp-content/uploads/2021/01/screenshot-2021-01-26-10-15-40-800x391.png)
In this article, we will look at a popular algorithm for hedge funds and high-frequency traders called pairs trading. In its most basic form, you select a pair of stocks that historically move together and trade when they diverge. The expectation is that as they return to a normal state, you will make money.
This is still a workable strategy for high frequency hedge fund traders who can co-locate giant server farms in exchange datacenters, but can it still work for average traders who don’t have these resources? Or are all of these statistical arbitrage opportunities gone by the time an average trader can execute? Can this strategy be run at a daily/weekly frequency anymore or does it have to be run in milliseconds?
We will run some tests on the basic strategy to see if it can work today.
Historical profitability of pairs trading
Pairs trading has been in use for decades, and has been profitable — even at weekly frequencies. In 2006, a study was done by Yale on its effectiveness. The study is worth reading: Pairs Trading: Performance of a Relative Value Arbitrage Rule.
We find that trading suitably formed pairs of stocks exhibits profits, which are robust to
Pairs Trading: Performance of a Relative Value Arbitrage Rule
conservative estimates of transaction costs. These profits are uncorrelated to the S&P 500,
however they do exhibit low sensitivity to the spreads between small and large stocks and
between value and growth stocks in addition to the spread between high grade and intermediate
grade corporate bonds and shifts in the yield curve. In addition to risk and transactions cost, we
rule out several explanations for the pairs trading profits, including mean-reversion as previously
documented in the literature, unrealized bankruptcy risk, and the inability of arbitrageurs to take
advantage of the profits due to short-sale constraints.
However, this study does find that opportunities are much less frequent and much less profitable in 2000- timeframe.
One view of the lower profitability of pairs trading in recent year is that returns are
Pairs Trading: Performance of a Relative Value Arbitrage Rule
competed away by increased hedge fund activity. The alternative view, taken in this paper, is that
abnormal returns to pairs strategies are a compensation to arbitrageurs for enforcing the “Law of
One Price”.
Building a pairs trading model
To determine whether pairs trading still works, we will model a basic pairs trading strategy in Python using historical data, and then see if we can use that strategy to generate excess return in the next period.
We will use a lot of loading code that we wrote in the Getting Started article, which you should read before this one.
Our first task is loading the data. Our data comes from Quandl in a set of CSV files. We will load them all into a DataFrame using pandas:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import quandl
import pickle
import csv
import os
from datetime import date
import sys
import statsmodels.api as sm
import scipy.optimize as sco
plt.style.use('fivethirtyeight')
np.random.seed(777)
alldata = pd.DataFrame()
try:
ticker_data = pd.read_csv("tickers.csv")
except FileNotFoundError as e:
pass
for t in ticker_data['ticker']:
try:
data = pd.read_csv("d:\\stockdata\\" + t + ".csv",
header = None,
usecols = [0, 1, 12],
names = ['ticker', 'date', 'adj_close'])
alldata = alldata.append(data)
except FileNotFoundError as e:
pass
Our ticker CSV file contains a lot of tickers that we don’t want to look at, such as delisted ones and OTC stocks, so we will filter it before loading:
ticker_data = ticker_data.loc[(ticker_data['table'] == 'SF1') & (ticker_data['isdelisted'] == 'N') & (ticker_data['currency'] == 'USD') & ((ticker_data.exchange == 'NYSE') | (ticker_data.exchange == 'NYSEMKT') | (ticker_data.exchange == 'NASDAQ'))]
Now, we have all of the relevant tickers in a DataFrame. The next step is cleaning the data so that we can build a correlation matrix. We will use daily data at first. Later, we can move to longer timeframes.
df = alldata.set_index('date')
table = df.pivot(columns='ticker')
table.columns = [col[1] for col in table.columns]
table.index = pd.to_datetime(table.index)
table = table['2018-01-01':'2020-01-01']
table = table.loc[:, (table.isnull().sum(axis=0) <= 30)]
table = table.dropna(axis='rows')
Finally, generating a correlation matrix is very simple with Pandas:
A AAL AAME AAN AAON AAP AAPL \
A 1.000000 -0.411075 -0.423860 0.548792 0.677535 0.439531 0.515594
AAL -0.411075 1.000000 0.762728 -0.675839 -0.625932 -0.729448 -0.526901
AAME -0.423860 0.762728 1.000000 -0.544478 -0.579686 -0.578142 -0.637582
AAN 0.548792 -0.675839 -0.544478 1.000000 0.857118 0.498967 0.648432
AAON 0.677535 -0.625932 -0.579686 0.857118 1.000000 0.484853 0.624596
... ... ... ... ... ... ...
ZIOP 0.296149 -0.085815 -0.192385 0.472562 0.574997 -0.224872 0.353245
ZIXI 0.440557 -0.699289 -0.566404 0.679136 0.761478 0.583238 0.284436
ZNGA 0.631641 -0.730482 -0.702510 0.844649 0.898749 0.453662 0.625134
ZUMZ 0.562601 -0.421862 -0.498312 0.619821 0.548948 0.285115 0.796054
ZVO -0.423629 0.493856 0.469000 -0.674794 -0.682076 -0.058555 -0.525241 Finding pair trading opportunities
With the correlation matrix, we can get a lot of information. Using a simple sort, we can get the top correlations:
XEL AEP 0.996523
V MA 0.994791
NEE ETR 0.994646
WEC XEL 0.994444
OPTT AEE -0.972316
SHIP AMT -0.972656
SO DYNT -0.972725
AEE FCEL -0.973476
OGE OPTT -0.976275As we can see, this is consistent with what the paper found: the most correlated stocks are for energy companies. Let’s look at one of these on a chart:
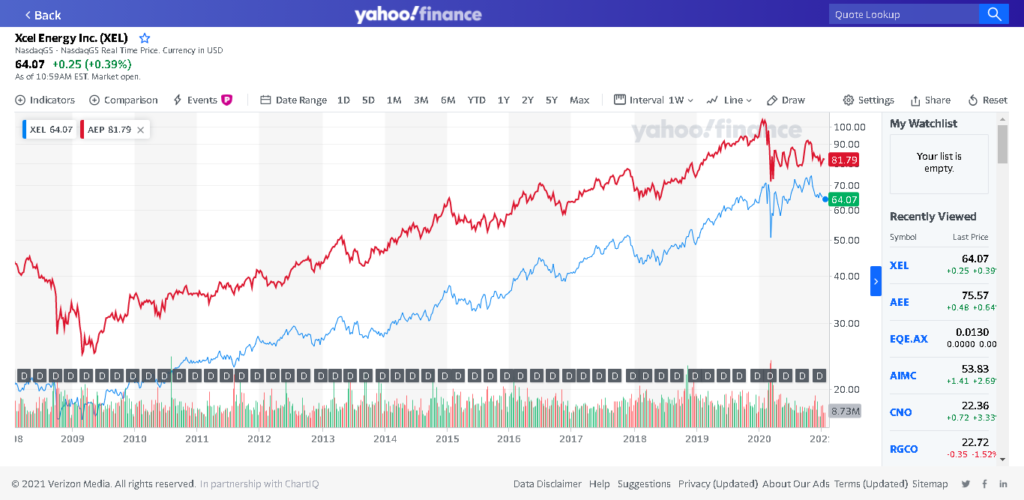
To determine the signal for when a trade should occur, we look at the difference between the two stocks:
In [22]: diff = table['XEL']-table['AEP'] In [23]: diff.mean() Out[23]: -24.10590632758745 In [24]: diff.std() Out[24]: 3.148618069119123
Now, we can say with a reasonably high level of confidence that if the two stocks diverge by more than 2 standard deviations (or ~ 6.3), there is a trading opportunity. Let’s see if that happens in the period following this one:
> next_period = df.pivot(columns='ticker')
> next_period.columns = [col[1] for col in next_period.columns]
> next_period.index = pd.to_datetime(next_period.index)
> next_period = next_period['2020-01-01':]
> next_diff = next_period['XEL']-next_period['AEP']
> next_diff.loc[next_diff < -30.4]
date
2020-01-15 -30.736753
2020-01-16 -30.877687
2020-01-17 -31.762922
2020-01-21 -31.903163
2020-01-22 -32.340503
2020-01-23 -32.607094
2020-01-24 -33.502785
2020-01-27 -33.378315
2020-01-28 -33.482761
2020-01-29 -33.890905
2020-01-30 -33.828830
2020-01-31 -33.521868
2020-02-03 -33.265412
2020-02-04 -32.095119
2020-02-05 -31.362759
2020-02-06 -30.806166
2020-02-07 -31.866599
2020-02-10 -32.091640
2020-02-11 -32.485245
2020-02-12 -31.993412
2020-02-13 -32.256399
2020-02-14 -32.717131
2020-02-18 -32.389837
2020-02-19 -31.938717
2020-02-20 -30.955869
So according to the pairs trading algorithm provided, we would open the trade on January 15, 2020 (XEL @ 63.59, AEP @ 94.33). The algorithm closes the trade when the two stocks cross their mean difference again. This happens on March 11, 2020 (XEL @ 65.90, AEP @ 88.21). This trade would therefore earn us $8.43, ignoring transaction costs.
A real test of the pairs trading algorithm
So in the one example, we did earn a positive return by following the pairs trading algorithm. The question is: does this generalize, and can we beat the market with this strategy? We will now look at a much larger number of correlated pairs.
First, we need to codify the trading algorithm. For readability, we will iterate over the DataFrames, although in practice there are much better ways to do this. We define a function to calculate per-trade profit
def calc_trade_profit(ticker1, ticker2, start_date, end_date):
if next_period.loc[start_date][ticker1] > next_period.loc[start_date][ticker2]:
high_ticker = ticker1
low_ticker = ticker2
else:
high_ticker = ticker2
low_ticker = ticker1
short_profit = next_period.loc[start_date][high_ticker] - next_period.loc[end_date][high_ticker]
long_profit = next_period.loc[end_date][low_ticker] - next_period.loc[start_date][low_ticker]
return long_profit + short_profit
Now, we iterate over each day in the period. For each day, we will iterate over the correlated pairs to find whether they trade on that day. If the difference between the prices of the two stocks is greater than the threshold (and was less yesterday), we open the trade. If the trade is open, and the difference between the prices goes below the mean, we close the trade.
Here’s our code:
print("starting trades")
for index, row in next_period.iterrows():
# iterate over the days of the next period
for sindex, srow in corrdata.iterrows():
# iterate over the correlated pairs
ticker1 = sindex[0]
ticker2 = sindex[1]
trade = ticker1 + '-' + ticker2
mean = srow['mean']
std = srow['std']
if not trade in trades:
trades[trade] = { 'open' : False, 'start' : None, 'earned' : 0. }
threshold = abs(mean) + 2*std
print(trade + " " + str(row[ticker1]) + " " + str(row[ticker2]) + " " + str(threshold) + " " + str(abs(row[ticker1] - row[ticker2])))
if ticker1 in prevrow:
if abs(row[ticker1] - row[ticker2]) > threshold and abs(prevrow[ticker1] - prevrow[ticker2] <= threshold):
#open a trade if not open
if not trades[trade]['open']:
print("opening trade " + ticker1 + "-" + ticker2 + ": " + str(index))
trades[trade]['start'] = index
trades[trade]['open'] = True
if abs(row[ticker1] - row[ticker2]) < abs(mean) and abs(prevrow[ticker1] - prevrow[ticker2]) >= abs(mean):
#close an open trade
if trades[trade]['open']:
print("closing trade " + ticker1 + "-" + ticker2 + ": " + str(index))
trades[trade]['earned'] = trades[trade]['earned'] + calc_trade_profit(ticker1, ticker2, trades[trade]['start'], index)
trades[trade]['start'] = None
trades[trade]['open'] = False
prevrow = row
Finally, we need to close all open trades on the last day (these are the ones that may be losers):
#now close all of the open trades on the last day of the period
last_day = next_period.index[-1]
for sindex, srow in corrdata.iterrows():
# iterate over the correlated pairs
ticker1 = sindex[0]
ticker2 = sindex[1]
trade = ticker1 + '-' + ticker2
if (trade in trades) and (trades[trade]['open']):
print("last day: closing trade " + ticker1 + "-" + ticker2)
trades[trade]['earned'] = trades[trade]['earned'] + calc_trade_profit(ticker1, ticker2, trades[trade]['start'], last_day)
trades[trade]['start'] = None
trades[trade]['open'] = False
print("total earned: " + str(functools.reduce(lambda acc,v: acc+trades[v]['earned'], trades, 0)))
Now, we run this algorithm on the top 100 correlated pairs:
XEL AEP 0.996523
V MA 0.994791
NEE ETR 0.994646
WEC XEL 0.994444
CMS 0.994384
SUI ELS 0.993536
CMS XEL 0.993018
AWK XEL 0.992827
UDR AVB 0.992741
AIV 0.992524
WEC AWK 0.992214
HE AEP 0.992158
SUI ETR 0.991948
MAA 0.991770
CMS LNT 0.991266
ADC O 0.991101
HE XEL 0.991046
OPTT FCEL 0.990808
AON AJG 0.990615
WELL PEAK 0.990414
AIV AVB 0.990408
TRNO PLD 0.990302
NEE LNT 0.990216
AEP AWK 0.989953
POR AEP 0.989822
CMS AEP 0.989687
O AIV 0.989058
UDR 0.989025
POR XEL 0.988931
PEAK O 0.988882
DRE EGP 0.988872
SO ETR 0.988799
DRE FR 0.988766
AWK AMT 0.988565
PNM XEL 0.988536
HE AWK 0.988447
ELS ETR 0.988435
O NNN 0.988409
EGP ELS 0.988395
MSFT V 0.988302
SUI NEE 0.987992
CMS POR 0.987979
CVV BLIN 0.987850
OGE AEE 0.987712
AEP WEC 0.987688
CMS AWK 0.987651
TRNO SUI 0.987628
PEAK ADC 0.987585
LNT ETR 0.987326
AEP PNM 0.987310
PEAK UDR 0.987200
POR AVB 0.987179
AVB CPT 0.987089
EQR ESS 0.986930
LNT WEC 0.986684
USM TDS 0.986674
WPC PSB 0.986629
NWE DTE 0.986558
CPT EQR 0.986507
AEE DTE 0.986407
XEL AMT 0.986397
EGP SUI 0.986270
ATO CMS 0.986256
NEE FE 0.986243
AEE NWE 0.986101
CMS EQR 0.986014
EGP STWD 0.985946
MA MSFT 0.985910
CMS FE 0.985907
NWE POR 0.985815
NEE ELS 0.985728
CCI AMT 0.985701
MT HAL 0.985365
EQR UDR 0.985344
MAA ETR 0.985262
MPW O 0.985165
EQR AVB 0.985094
BAH ARCC 0.984924
MA FICO 0.984884
HE WEC 0.984878
AEP AMT 0.984747
SUI SO 0.984630
NEE SO 0.984616
WEC ETR 0.984588
PNM AWK 0.984569
FR TRNO 0.984532
HE PNM 0.984259
BKH NWE 0.984165
STE BAH 0.984014
AWR WEC 0.983979
V ARCC 0.983937
UDR ADC 0.983922
MAA TRNO 0.983697
PSB WELL 0.983626
MAA NEE 0.983566
VRSK MSI 0.983533
BAH V 0.983492
HE AMT 0.983375
AWK POR 0.983327
FE LNT 0.983292Results of the pairs trading algorithm
From the period of January 1, 2020 to August 18, 2020, the algorithm would have earned a profit of $284, by trading one long and one short share at each signal. Since each long is paired with a larger short, you could achieve this with essentially $0 initial investment (ignoring trading costs), making the return essentially infinite. Moreover, if you run the model from January 1, 2020 to April 1, 2020, you would have seen a significant profit, even while the S&P 500 had dropped by almost 25%.
However, in reality, whenever you open a short position, you assume a liability.
Conclusion: does pairs trading still work in 2021?
Our model shows that pairs trading can work and be profitable in 2021. The question of how profitable, and whether it is worth the risk is something we will tackle in a future article.

No Comments