In this article we will take a look at principal component analysis. Principal component analysis (or PCA) is a tool used in many disciplines to find patterns in data. It can either be used as part of a machine learning algorithm, or it can be used on its own.

What is principal component analysis?

Wikipedia defines principal component analysis like this:

Principal component analysis (PCA) is the process of computing the principal components and using them to perform a change of basis on the data, sometimes using only the first few principal components and ignoring the rest.

Wikipedia

Essentially, it uses matrices and eigenvectors/eigenvalues to find vectors which together can span most of the solution space. We won’t get too much into the math behind it, but we have linked to some useful articles below.

Several academic papers have suggested that this type of analysis can generate factors which predict asset prices. In this article we will determine if that’s still true.

Suggested readings

• Performance measurement with the arbitrage pricing theory
• Risk and return in equilibrium APT
• Linear algebra review (if you want to understand the math)
• Getting started: using Python to find alpha [2021]
• Do CAPM efficient portfolios really outperform random ones? [2021]

Modeling stock returns with 2 factor PCA

We begin with a basic model of stock returns. We will limit this model to three months: 2 input months and one month to test the results.

There are different ways to use PCA on stock data. We can use the stocks as features and the stock prices at certain dates as samples, or we can use the dates as features and each stock as a sample. Each way provides valuable information.

In the papers linked above, the authors build a matrix with time periods as columns and stocks as rows to perform their PCA. We use the following code to create a similar matrix:

 
alldata = pd.DataFrame()

pd.set_option('display.max_rows', 100)
pd.set_option('display.max_columns', 100)


tickers = pd.read_csv("tickers.csv")
tickers = tickers.loc[(tickers.exchange == 'NYSE') | (tickers.exchange == 'NYSEARCA')| (tickers.exchange == 'NYSEMKT')| (tickers.exchange == 'NASDAQ')]
tickers = tickers.loc[tickers.isdelisted == 'N']
tickers = tickers.loc[tickers.table == 'SF1']

for t in tickers['ticker']:
    print(t)
    try:
        data = pd.read_csv(t + ".csv", 
                            header = None,
                            usecols = [0, 1, 12],
                            names = ['ticker', 'date', 'adj_close'])
    
        alldata = alldata.append(data)
        
    except FileNotFoundError as e:
        pass



df = alldata.set_index('date')


table = df.pivot(columns='ticker')
table.columns = [col[1] for col in table.columns]

#table = table['2010-01-04':'2020-08-18']
table = table['2014-01-01':]

table.index = pd.to_datetime(table.index)
table.fillna(1, inplace=True)



table.resample('BM').last()
t = table.resample('BM').last().pct_change().transpose()

t = t[['2019-06-28','2019-07-31','2019-08-30']]

x = t[['2019-06-28','2019-07-31']]
y = t['2019-08-30']

This gives us all stocks and their percent changes as rows, and the three dates in 2019 as columns. Now let’s use sklearn’s PCA function to run a 2 dimension PCA. In this code we first scale the data using the StandardScaler, and run the PCA to get a DataFrame of principal vectors:

x = pre.StandardScaler().fit_transform(x)
pca = dec.PCA(n_components = 2)
vectors = pca.fit_transform(x)

That’s it! The actual PCA is done. The vectors array now contains the 2 vectors that the PCA function believes are the principal factors that explain the data.

We would really like (at least with this first test) to visualize the data to see what exactly the PCA function did. Let’s plot the vectors (the x and y axis) along with whether the returns are positive (shown in red) or negative (shown in black) over the period. If the PCA function successfully found explanatory components, we should see some separation of the data:

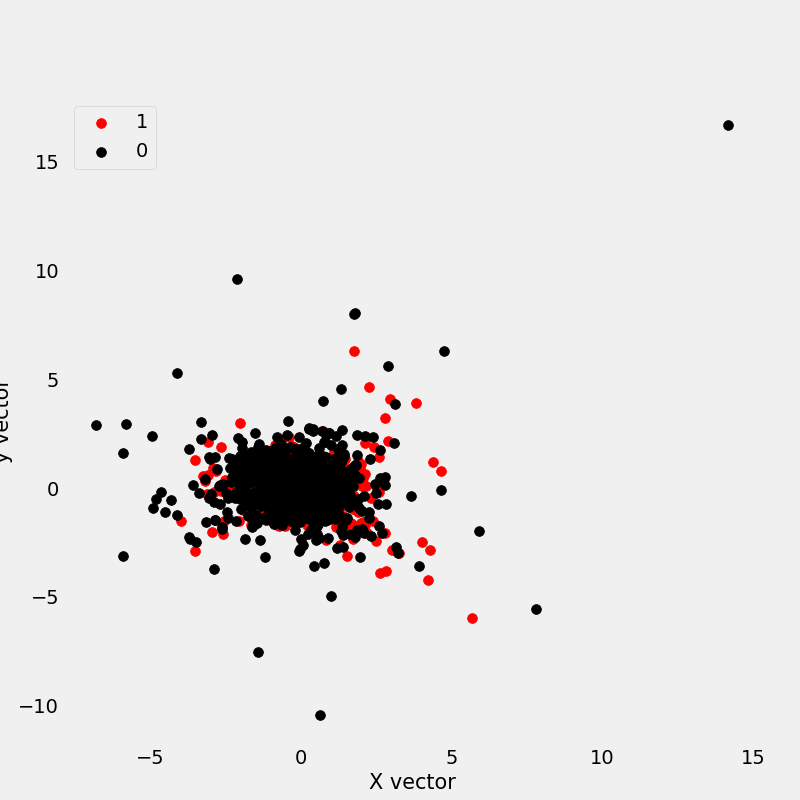
Hm…this does not look too promising. You immediately notice that the red and black points are nearly all intermingled. The PCA was not able to separate this data into an X and Y that predicts the stock returns.

At this point, we could use a predictive tool such as regression or machine learning to make a prediction using the extracted factors. Unfortunately, PCA doesn’t help us achieve a better prediction.

Can we do better with more factors?

We can add more factors and more samples, but the predictive value is not enhanced. Regardless of whether we use individual time points as samples or stocks as samples and times as factors, PCA does not show statistically significant predictive value.

Conclusion

Principal component analysis is extremely useful looking backward in order to analyze data. However, for prediction of stock prices, it isn’t particularly helpful.